Berechnungsgrundlagen - Auslegung von Industriestoßdämpfern
ACE Stoßdämpfer verzögern linear und sind damit den herkömmlichen Dämpfungselementen weit überlegen. Mit Hilfe der Übersicht zu den Berechnungsgrundlagen zur Auslegung eines Stoßdämpfers sind Sie in der Lage den richtigen Industriestoßdämpfer für Ihr Projekt aus dem ACE Webkatalog auszuwählen.
Welche Daten sind notwendig?
Ca. 90 % der Einsatzfälle lassen sich mit folgenden fünf Angaben einfach berechnen:
- Abzubremsende Masse (Gewicht) m [kg]
- Aufprall- oder Auffahrgeschwindigkeit vD [m/s]
- Evtl. vorhandene zusätzliche Antriebskraft F [N]
- Anzahl der Hübe oder Takte pro Stunde x [1/h]
- Anzahl Stoßdämpfer parallel n
Verwendete Formelzeichen
| Kürzel | Einheit | Beschreibung | Kürzel | Einheit | Beschreibung |
|---|---|---|---|---|---|
| W1 | Nm | kinetische Energie pro Hub; nur Massenbelastung | 3HM | 1 bis 3 | Haltemoment-Faktor (normal 2,5) |
| W2 | Nm | Energie/Arbeit der Antriebskraft pro Hub | M | Nm | Drehmoment |
| W3 | Nm | Gesamtenergie pro Hub (W1 + W2) | J | kgm2 | Massenträgheitsmoment |
| 1W4 | Nm/h | Gesamtenergie pro Stunde (W3 · x) | g | m/s2 | Erdbeschleunigung = 9,81 |
| me | kg | effektive Masse | h | m | Fallhöhe ohne Stoßdämpferhub |
| m | kg | abzubremsende Masse | s | m | Stoßdämpferhub |
| n | Anzahl Stoßdämpfer (parallel) | L/R/r | m | Radius | |
| 2v | m/s | Geschwindigkeit beim Aufprall | Q | N | Gegenkraft/Stützkraft |
| 2vD | m/s | Aufprallgeschwindigkeit am Stoßdämpfer | μ | Reibwert | |
| ω | rad/s | Winkelgeschwindigkeit beim Aufprall | t | s | Abbremszeit |
| F | N | zusätzliche Antriebskraft | a | m/s2 | Verzögerung |
| x | 1/h | Anzahl der Hübe pro Stunde | α | ° | Auftreffwinkel |
| P | kW | Motorleistung | β | ° | Winkel |
1 Die in den jeweiligen Leistungstabellen aufgeführten zulässigen W4 Werte gelten nur bei Raumtemperatur. Bei höheren Umgebungsbedingungen ergeben sich reduzierte Werte.
2 v bzw. vD ist die Endgeschwindigkeit der Masse. Bei beschleunigter Bewegung ist deshalb ein Zuschlag von 50-100% auf die Durchschnittsgeschwindigkeit einzuplanen.
3 HM =^ Verhältnis Anzugsmoment zum Nennmoment des Motors (bauartbedingt)
Die Auswahl der Stoßdämpfer aus der Leistungstabelle erfolgt bei allen Beispielen nach W3, W4, me und dem gewählten Stoßdämpferhub s.
Für alle Beispiele gilt:
Bei Verwendung von mehreren Dämpfern parallel teilen sich die Werte W3, W4 und me entsprechend der Dämpfer auf.
|
Gegenkraft/Stützkraft Q [N] Q = (1,5 · W3) / s |
Abbremszeit t [s] t = (2,6 · s) / vD |
Verzögerung a [m/s2] a = (0,75 · vD2) / s |
Die Formeln zur Berechnung der Gegenkraft, Abbremszeit und Verzögerung beziehen sich nur auf ACE Industriestoßdämpfer. Bei einstellbaren ACE Industriestoßdämpfern gelten diese 3 Formeln nur bei richtiger Einstellung. Sicherheit vorsehen. Bei Sicherheitsstoßdämpfern gelten andere Formeln. In diesem Fall wenden Sie sich bitte an ACE.
Einsatzfälle
| Einsatzfall | Formel | Beispiel | |
|---|---|---|---|
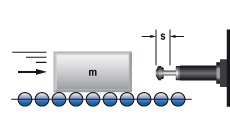
1. Masse ohne Antriebskraft
|
W1 = m · v2 · 0,5
W2 = 0
W3 = W1 + W2
W4 = W3 · x
vD = v
me = m
|
m = 100 kg W1 = 100 · 1,52 · 0,5 = 113 Nm |
|
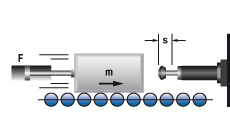
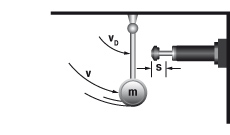
2. Masse mit Antriebskraft
|
W1 = m · v2 · 0,5
W2 = F · s
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
2.1 bei senkrechter Bewegung nach oben
W2 = (F – m · g) · s
2.2 bei senkrechter Bewegung nach unten
W2 = (F + m · g) · s
|
m = 36 kg
1v = 1,5 m/s
F = 400 N
x = 1000 1/h
s = 0,025 m (gewählt)
W1 = 36 · 1,52 · 0,5 = 41 Nm
W2 = 400 · 0,025 = 10 Nm
W3 = 41 + 10 = 51 Nm
W4 = 51 · 1000 = 51000 Nm/h
me = 2 · 51 : 1,52 = 45 kg
1 v ist die Endgeschwindigkeit der Masse:
Bei pneumatischem Antrieb ist deshalb ein Zuschlag von 50-100% auf die Durchschnittsgeschwindigkeit einzuplanen. |
|
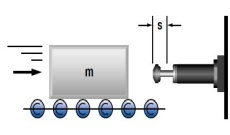
3. Masse mit Antriebskraft (formschlüssig)
|
W1 = m · v2 · 0,5
W2 = (1000 · P ·HM · s) / v
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
|
m = 800 kg W1 = 800 · 1,22 · 0,5 = 576 Nm Getriebe, soweit nicht vernachlässigbar, zu W1 addieren.. |
|
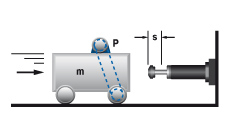
4. Masse auf angetriebenen Rollen (reibschlüssig)
|
W1 = m · v2 · 0,5
W2 = m · μ · g · s
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
|
m = 250 kg W1 = 250 · 1,52 · 0,5 = 281 Nm |
|
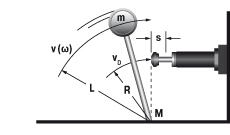
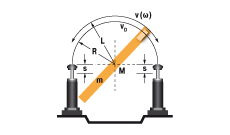
5. Schwenkende Masse mit Antriebsmoment
|
W1 = m · v2 · 0,5 = 0,5 · J · ω2
W2 = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
m = 20 kg W1 = 20 · 12 · 0,5 = 10 Nm |
|
6. Frei fallende Masse
|
W1 = m · g · h
W2 = m · g · s
W3 = W1 + W2
W4 = W3 · x
vD = √2 · g · h
me = (2 · W3) / vD2
|
m = 30 kg W1 = 30 · 0,5 · 9,81 = 147 Nm |
|
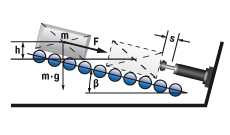
6.1 Masse auf schiefer Ebene
|
W1 = m · g · h = m · vD2 · 0,5
W2 = m · g · sinβ · s
W3 = W1 + W2
W4 = W3 · x
vD = √2 · g · h
me = (2 · W3) / vD2
6.1a bei senkrechter Bewegung nach oben
W2 = (F – m · g· sinβ) · s
6.1b bei senkrechter Bewegung nach unten
W2 = (F + m · g· sinβ) · s
|
m = 500 kg W1 = 500 · 9,81 · 0,1 = 490,5 Nm |
|
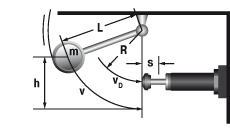
6.2 Masse an Drehpunkt, frei schwingend
|
W1 = m · g · h
W2 = 0
W3 = W1 + W2
W4 = W3 · x
vD = √2 · g · h · (R / L)
me = (2 · W3) / vD2
tan α = s / R
|
m = 50 kg W1 = 50 · 9,81 · 1 = 490,5 Nm |
|
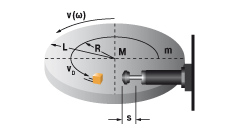
7. Drehtisch mit Antriebsmoment, horizontal oder vertikal
|
W1 = m · v2 · 0,25 = 0,5 · J · ω2
W2 = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
m = 1000 kg W1 = 1000 · 1,12 · 0,25 = 303 Nm |
|
8. Schwenkende Masse mit Antriebsmoment (z. B. Wendeeinrichtung)
|
W1 = m · v2 · 0,17 = 0,5 · J · ω2
W2 = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
J = 56 kgm2 W1 = 0,5 · 56 · 12 = 28 Nm |
|
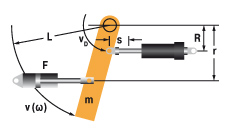
9. Schwenkende Masse mit Antriebskraft
|
W1 = m · v2 · 0,17 = 0,5 · J · ω2
W2 = (F · r · s) / R = (M · s) / R
W3 = W1 + W2
W4 = W3 · x
vD = (v · R) / L = ω · R
me = (2 · W3) / vD2
|
m = 1000 kg W1 = 1000 · 22 · 0,17 = 680 Nm |
|
10. Abgesenkte Masse ohne Antriebskraft
|
W1 =m · v2 · 0,5
W2 = m · g · s
W3 = W1 + W2
W4 = W3 · x
vD = v
me = (2 · W3) / vD2
|
m = 6000 kg W1 = 6000 · 1,52 · 0,5 = 6750 Nm |
|
Effektive Masse (me)
Die effektive Masse (me) kann die tatsächlich in Bewegung befindliche Masse (Beispiel A und C) oder eine rechnerische Ersatzmasse für die Antriebskraft oder Übersetzung plus tatsächlicher Masse (Beispiel B und D) sein.
| Einsatzfall | Beispiel |
|---|---|
A Masse ohne Antriebskraft
|
m = 100 kg
vD = v = 2 m/s
W1 = W3 = 200 Nm
me = (2 · 200) / 4 = 100 kg
FORMEL: ME = M
|
B Masse mit Antriebskraft
|
m = 100 kg
F = 2000 N
vD = v = 2 m/s
s = 0,1 m
W1 = 200 Nm
W2 = 200 Nm
W3 = 400 Nm
me = (2 · 400) / 4 = 200 kg
FORMEL: ME = (2 · W3) / VD2
|
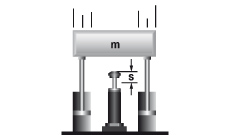
C Masse ohne Antriebskraft direkt auf den Stoßdämpfer
|
m = 20 kg
vD = v = 2 m/s
W1 = W3 = 40 Nm
me = (2 · 40) / 22 = 20 kg
FORMEL: ME = M
|
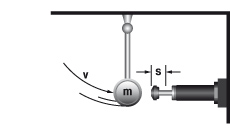
D Masse ohne Antriebskraft mit Hebelübersetzung
|
m = 20 kg
v = 2 m/s
vD = 0,5 m/s
s = 0,1 m
W1 = W3 = 40 Nm
me = (2 · 40) / 0,52 = 320 kg
FORMEL: ME = (2 · W3) / VD2
|